| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 데이터
- 파이썬
- 자동매매프로그램
- 패캠챌린지
- EDA
- airflow
- 방콕여행
- API
- 딥러닝
- 데이터 분석
- 직장인인강
- 챗지피티
- 빅데이터
- 상관분석
- Ai
- Python
- 패스트캠퍼스
- 활성화함수
- DAGs
- 리뷰
- 머신러닝
- 분석
- 패스트캠퍼스후기
- 독서리뷰
- correlation
- 에어플로
- 파이썬을활용한시계열데이터분석A-Z올인원패키지
- 태국여행
- 직장인자기계발
- 데이터분석
- Today
- Total
데이터를 기반으로
상관계수의 기초 - 피어슨 상관계수(Pearson correlation)(1) 본문
이전 글에서 공분산과 상관계수에 대한 차이를 알아보았다.
공분산과 상관계수의 차이 - (1)
이전 게시글에서 변수 타입에 대해 정의를 내려보았다. 그럼 이제 각 변수들 간의 어떠한 관계가 있을 건지에 대한 궁금증이 생기기 마련이다. 우리는 어떠한 특정 현상이나 관계에 대해 가장
ds92.tistory.com
공분산과 상관계수의 차이 - (2)
1번 글에 이어서 상관계수의 개념을 보면서 시작하고자 한다. [ 상관 계수(Correlation coefficient) ] 상관계수(相關係數, correlation coefficient)는 두 변수 사이의 통계적 관계를 표현하기 위해 특정한 상
ds92.tistory.com
이번 글에서는 상관계수의 대명사이자 가장 흔하게 상관계수를 구할 때 사용하는 방법인 바로 '피어슨 상관계수' 이다.
이번 글을 작성하고자 공부하면서, 기존에 내가 구했던 상관계수도 조금씩 틀렸던 부분을 발견할 수 있었다.
상관계수에 대한 개념은 위에서 확인했기에, 이번 글에서는 오직 '피어슨' 상관계수에만 포커싱을 가지며 작성할 계획이다.
[ 피어슨 상관 계수 란? ]
통계학에서 , 피어슨 상관 계수(Pearson Correlation Coefficient ,PCC)란 두 변수 X 와 Y 간의 선형 상관 관계를 계량화한 수치다. 피어슨 상관 계수는 코시-슈바르츠 부등식에 의해 +1과 -1 사이의 값을 가지며, +1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계 없음, -1은 완벽한 음의 선형 상관 관계를 의미한다. 일반적으로 상관관계는 피어슨 상관관계를 의미하는 상관계수이다.
- 출처 : 위키백과 -

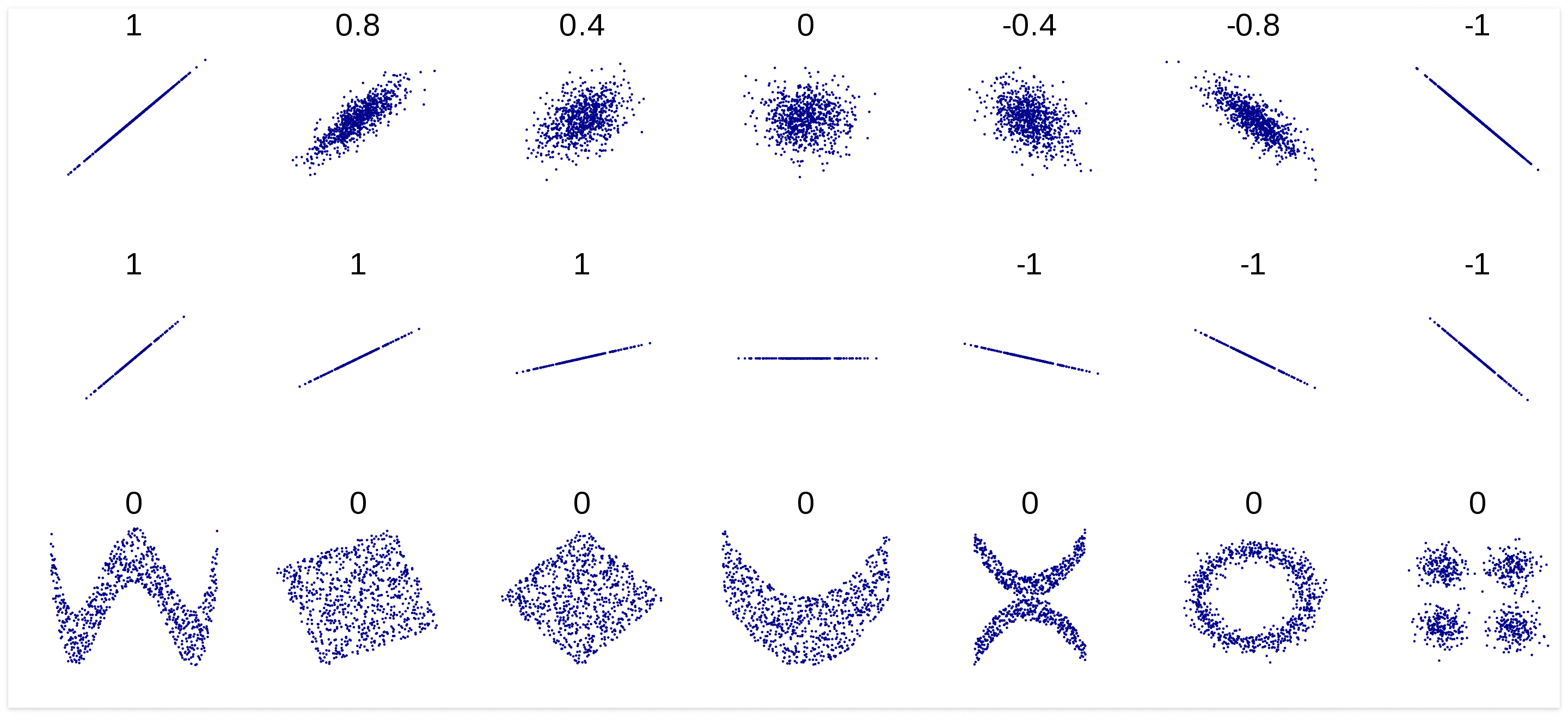
위 그래프 산점도 위에 숫자들이 곧 상관 계수이다.
y=x 그래프 스러울 수록 1에 가깝고, y=-x 그래프와 비슷할 수록 -1 에 가까운 수치가 산정된다.
우리가 상관계수를 추출하여 관련이 있는지 보고자하는 2개의 집단에 대한 가정들이 몇개있다. 이러한 가정들을 만족해야 비로소 상관계수라는 척도로 두 변수 사이에 대한 관계를 탐색할 수 있는 것이다.
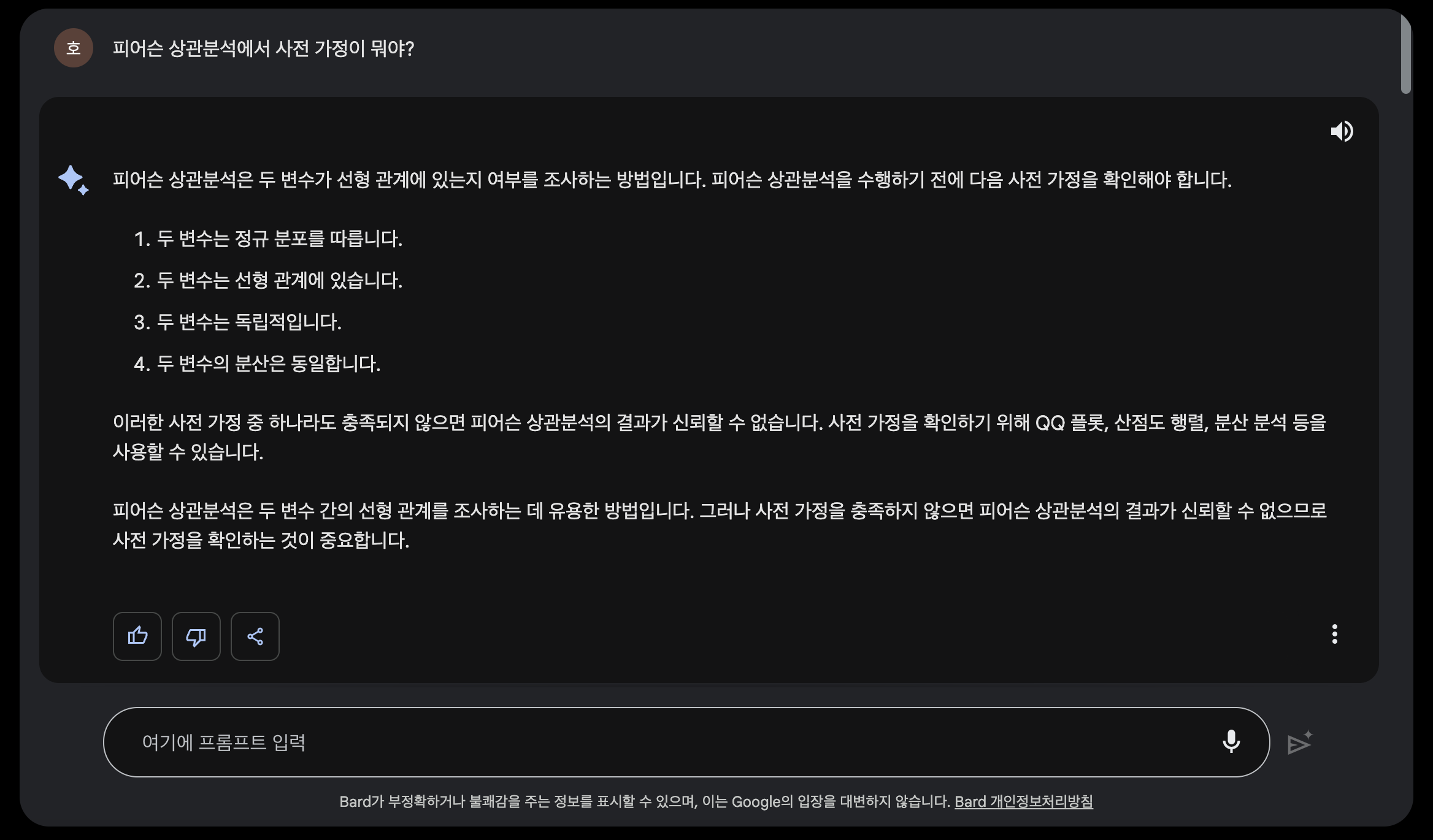
먼저, 내가 알고 있는 상관 계수를 사용하기 전 사전 가정으로 알고 있던 내용이 최근 유행인 생성형 AI들은 어떻게 답변을 내놓을 지 궁금하여 직접 질문을 해보았다.
아레는 구글에서 제공하는 바드에게 물어보니 아래와 같은 답변을 받았다.
아래의 사진은 chat GPT 에게 질문한 답변이다.

이렇게 여러가지에 대한 가정들이 나오는 것을 확인할 수 있었다.
심지어 여러 논문에서는 이러한 가정을 만족하는지 조차도 확인하지 않고 지나간 논문들도 꽤 많아서 어떤게 맞는 것인지 찾기 어려운 부분이 있었다.
많은 서칭을 통해 가장 피어슨 상관 계수에 대한 사전 정의를 명확하게 설명해주는 저널을 발견했다.
https://academic.oup.com/ckj/article/14/11/2332/6262634
Conducting correlation analysis: important limitations and pitfalls
Abstract. The correlation coefficient is a statistical measure often used in studies to show an association between variables or to look at the agreement betwee
academic.oup.com
해당 사이트에 존재하는 위 저널이 가장 잘 설명해주는 것을 확인할 수 있었다.
위 저널에서 설명하는 피어슨 상관계수를 사용할 수 있는 사전 가정은 크게 4가지였다.
[ 상관계수 사전 가정 ]
1. 두 변수는 모두 정규 분포를 따르는가?
→ 더 명확하게 말하면, 이변량 정규분포(bivariate normal distribute)를 만족하는가?
→ 모수적인 방법이라 정규분포가 가정되어야 한다.
2. 이상치들이 존재하지 않는가?
→ 상관 계수는 이상치에 민감하게 반응하기에, 데이터의 이상치를 제거하고 진행해야한다.
3. 두 변수 모두 연속형 변수인가?
4. 선형관계에 있는가?
→ 산점도를 통해 육안으로 확인해보는 방식을 선호하지만, 더욱 정확하게 진행하고자 한다면 선형회귀분석을 통해 선형성을 검증해보는
것도 좋다.
위 가정 중 먼저 y=x 그래프와 y=x^2 그래프의 데이터를 생성하여, 각각의 상관계수를 추출해보고자 한다.
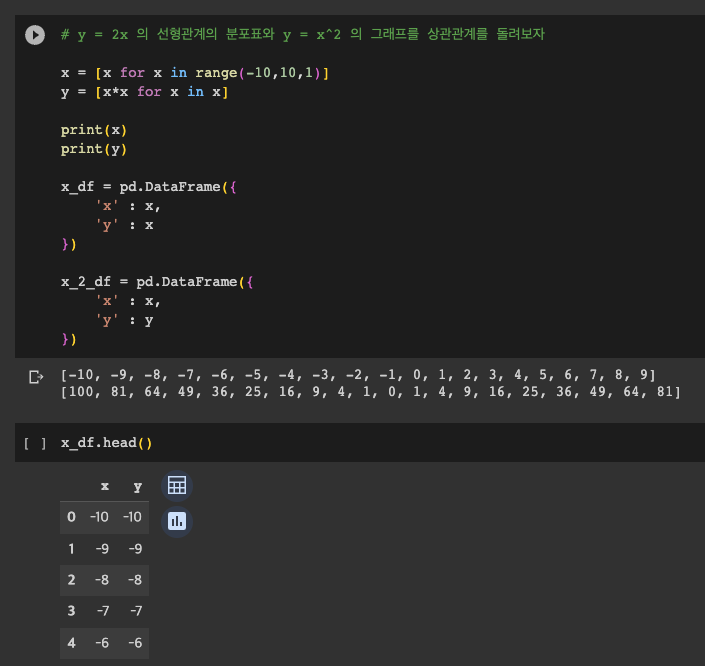
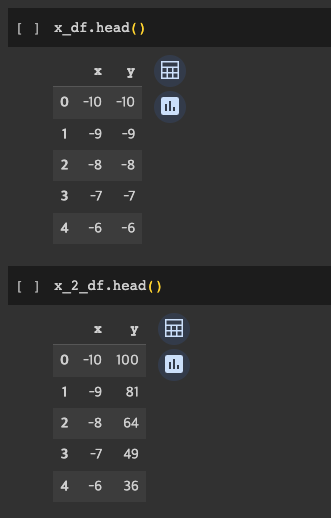
x_df 는 y=x 그래프에 맞춘 데이터 프레임이고, x_2_df 는 y=x^2에 맞춘 그래프이다.
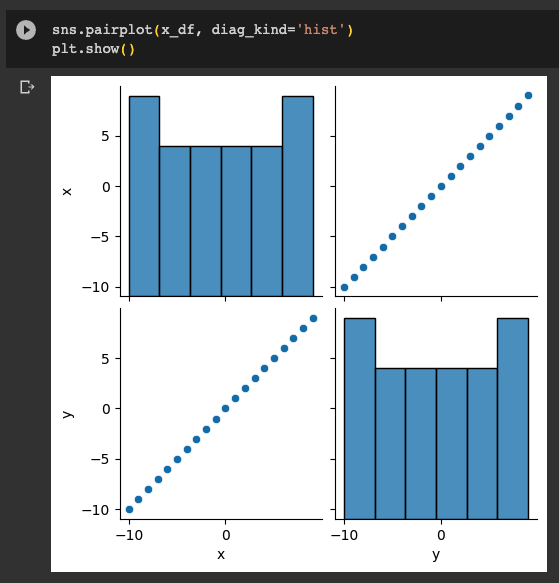
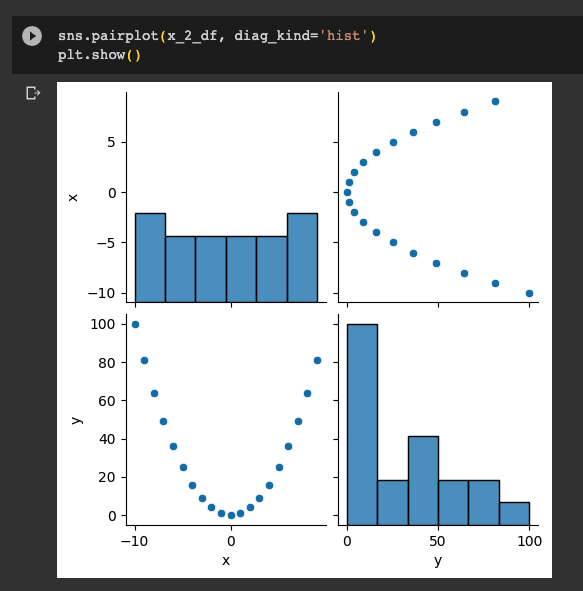
각 그래프를 그려보니, 위와 같이 원하던 방향으로 잘 분포되어 있는 것을 확인할 수 있었다.
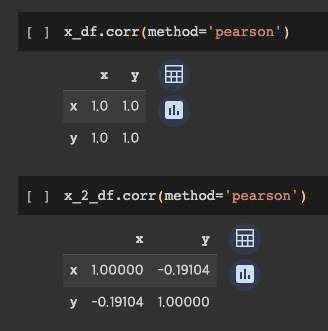
마지막 상관계수를 추출해보면 위와 같이 곡선인 y=x2 의 그래프는 당연하게도 상관계수가 0에 가까운 -0.1이 나온것을 확인할 수 있었다.
정확하게 표현하는 법은 아니지만 단순하게 표현한다면 곡선 그래프는 선형관계가 되기 쉽지 않다. 그러므로 위와 같은 결과가 보여진 것을 알 수 있었다.
이러한 특성을 보이고 있다고 생각하면 될 것 같고 글이 길어져서, 2번째 글로 이어서 설명할 예정이다.
실제 데이터셋을 기반으로 진행해보고, 정규성 검정까지 정리할 예정이다.
'통계 > 통계관련 개념' 카테고리의 다른 글
| 공분산과 상관계수의 차이 - (2) (0) | 2023.08.16 |
|---|---|
| 공분산과 상관계수의 차이 - (1) (0) | 2023.08.15 |
| 변수(Variable)의 개념 및 종류 (0) | 2023.07.30 |
| 선형(Linearity)과 비선형(Non-linearity)의 차이점 (0) | 2022.09.02 |



